Conditional quantile estimates for model evaluation

Function to calculate conditional quantiles with flexible conditioning. The function is for use in model evaluation and more generally to help better understand forecast predictions and how well they agree with observations.

Usage

conditionalQuantile(
  mydata,
  obs = "obs",
  mod = "mod",
  type = "default",
  bins = 31,
  min.bin = c(10, 20),
  xlab = "predicted value",
  ylab = "observed value",
  col = brewer.pal(5, "YlOrRd"),
  key.columns = 2,
  key.position = "bottom",
  auto.text = TRUE,
  ...
)

Arguments

mydata

A data frame containing the field obs and mod representing observed and modelled values.

obs

The name of the observations in mydata.

mod

The name of the predictions (modelled values) in mydata.

type

type determines how the data are split i.e. conditioned, and then plotted. The default is will produce a single plot using the entire data. Type can be one of the built-in types as detailed in cutData e.g. “season”, “year”, “weekday” and so on. For example, type = "season" will produce four plots --- one for each season.

It is also possible to choose type as another variable in the data frame. If that variable is numeric, then the data will be split into four quantiles (if possible) and labelled accordingly. If type is an existing character or factor variable, then those categories/levels will be used directly. This offers great flexibility for understanding the variation of different variables and how they depend on one another.

Type can be up length two e.g. type = c("season", "weekday") will produce a 2x2 plot split by season and day of the week. Note, when two types are provided the first forms the columns and the second the rows.

bins

Number of bins to be used in calculating the different quantile levels.

min.bin

The minimum number of points required for the estimates of the 25/75th and 10/90th percentiles.

xlab

label for the x-axis, by default “predicted value”.

ylab

label for the y-axis, by default “observed value”.

col

Colours to be used for plotting the uncertainty bands and median line. Must be of length 5 or more.

key.columns

Number of columns to be used in the key.

key.position

Location of the key e.g. “top”, “bottom”, “right”, “left”. See lattice xyplot for more details.

auto.text

Either TRUE (default) or FALSE. If TRUE titles and axis labels etc. will automatically try and format pollutant names and units properly e.g. by subscripting the `2' in NO2.

...

Other graphical parameters passed onto cutData and lattice:xyplot. For example, conditionalQuantile passes the option hemisphere = "southern" on to cutData to provide southern (rather than default northern) hemisphere handling of type = "season". Similarly, common axis and title labelling options (such as xlab, ylab, main) are passed to xyplot via quickText to handle routine formatting.

Details

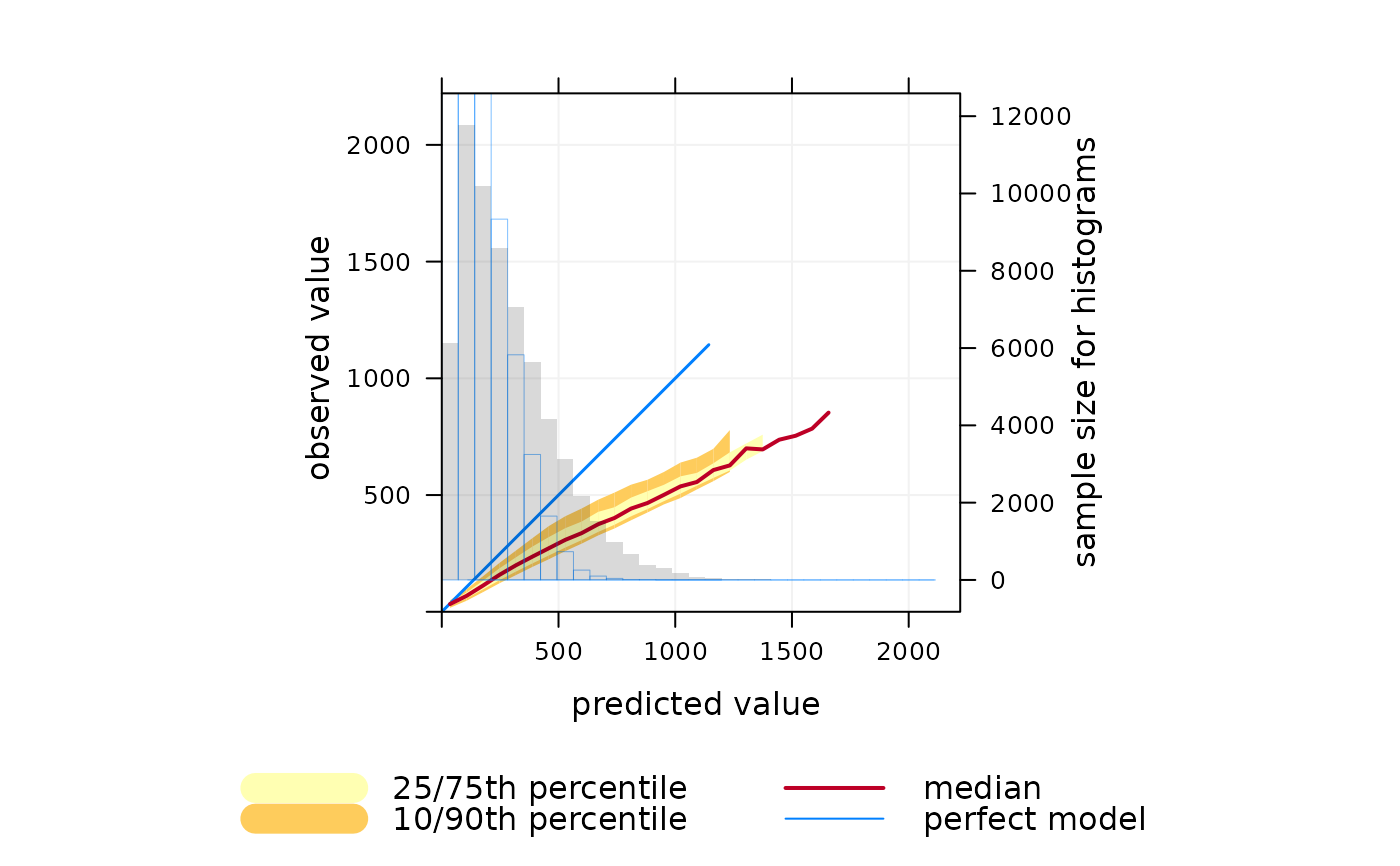
Conditional quantiles are a very useful way of considering model performance against observations for continuous measurements (Wilks, 2005). The conditional quantile plot splits the data into evenly spaced bins. For each predicted value bin e.g. from 0 to 10~ppb the corresponding values of the observations are identified and the median, 25/75th and 10/90 percentile (quantile) calculated for that bin. The data are plotted to show how these values vary across all bins. For a time series of observations and predictions that agree precisely the median value of the predictions will equal that for the observations for each bin.

The conditional quantile plot differs from the quantile-quantile plot (Q-Q plot) that is often used to compare observations and predictions. A Q-Q~plot separately considers the distributions of observations and predictions, whereas the conditional quantile uses the corresponding observations for a particular interval in the predictions. Take as an example two time series, the first a series of real observations and the second a lagged time series of the same observations representing the predictions. These two time series will have identical (or very nearly identical) distributions (e.g. same median, minimum and maximum). A Q-Q plot would show a straight line showing perfect agreement, whereas the conditional quantile will not. This is because in any interval of the predictions the corresponding observations now have different values.

Plotting the data in this way shows how well predictions agree with observations and can help reveal many useful characteristics of how well model predictions agree with observations --- across the full distribution of values. A single plot can therefore convey a considerable amount of information concerning model performance. The conditionalQuantile function in openair allows conditional quantiles to be considered in a flexible way e.g. by considering how they vary by season.

The function requires a data frame consisting of a column of observations and a column of predictions. The observations are split up into bins according to values of the predictions. The median prediction line together with the 25/75th and 10/90th quantile values are plotted together with a line showing a “perfect” model. Also shown is a histogram of predicted values (shaded grey) and a histogram of observed values (shown as a blue line).

Far more insight can be gained into model performance through conditioning using type. For example, type = "season" will plot conditional quantiles by each season. type can also be a factor or character field e.g. representing different models used.

See Wilks (2005) for more details and the examples below.

References

Murphy, A. H., B.G. Brown and Y. Chen. (1989) Diagnostic Verification of Temperature Forecasts, Weather and Forecasting, Volume: 4, Issue: 4, Pages: 485-501.

Wilks, D. S., 2005. Statistical Methods in the Atmospheric Sciences, Volume 91, Second Edition (International Geophysics), 2nd Edition. Academic Press.

See also

The verification package for comprehensive functions for forecast verification.

Other model evaluation functions: TaylorDiagram(), conditionalEval(), modStats()

Author

David Carslaw

Examples

## make some dummy prediction data based on 'nox'
mydata$mod <- mydata$nox * 1.1 + mydata$nox * runif(1:nrow(mydata))

# basic conditional quantile plot
## A "perfect" model is shown by the blue line
## predictions tend to be increasingly positively biased at high nox,
## shown by departure of median line from the blue one.
## The widening uncertainty bands with increasing NOx shows that
## hourly predictions are worse for higher NOx concentrations.
## Also, the red (median) line extends beyond the data (blue line),
## which shows in this case some predictions are much higher than
## the corresponding measurements. Note that the uncertainty bands
## do not extend as far as the median line because there is insufficient
# to calculate them
conditionalQuantile(mydata, obs = "nox", mod = "mod")


## can split by season to show seasonal performance (not very
## enlightening in this case - try some real data and it will be!)

if (FALSE) {
conditionalQuantile(mydata, obs = "nox", mod = "mod", type = "season")
}